日常では 0 〜 9 までの数字によって表す 10 進法を使用しますが、コンピューターは 0 と 1 の 2 種類の数字だけで数を表す。
- 10 進法は「10」で繰り上がる ・・・ 109 に 1 を足すと 110
- 2 進法は「2」で繰り上がる ・・・ 101 に 1 を足すと 110
10 進法と 2 進法
| 10進法 |
2進法 |
10進法 |
2進法 |
| 1 |
1 |
51 |
110011 |
| 2 |
10 |
52 |
110100 |
| 3 |
11 |
53 |
110101 |
| 4 |
100 |
54 |
110110 |
| 5 |
101 |
55 |
110111 |
| 6 |
110 |
56 |
111000 |
| 7 |
111 |
57 |
111001 |
| 8 |
1000 |
58 |
111010 |
| 9 |
1001 |
59 |
111011 |
| 10 |
1010 |
60 |
111100 |
| 11 |
1011 |
61 |
111101 |
| 12 |
1100 |
62 |
111110 |
| 13 |
1101 |
63 |
111111 |
| 14 |
1110 |
64 |
1000000 |
| 15 |
1111 |
65 |
1000001 |
| 16 |
10000 |
66 |
1000010 |
| 17 |
10001 |
67 |
1000011 |
| 18 |
10010 |
68 |
1000100 |
| 19 |
10011 |
69 |
1000101 |
| 20 |
10100 |
70 |
1000110 |
| 21 |
10101 |
71 |
1000111 |
| 22 |
10110 |
72 |
1001000 |
| 23 |
10111 |
73 |
1001001 |
| 24 |
11000 |
74 |
1001010 |
| 25 |
11001 |
75 |
1001011 |
| 26 |
11010 |
76 |
1001100 |
| 27 |
11011 |
77 |
1001101 |
| 28 |
11100 |
78 |
1001110 |
| 29 |
11101 |
79 |
1001111 |
| 30 |
11110 |
80 |
1010000 |
| 31 |
11111 |
81 |
1010001 |
| 32 |
100000 |
82 |
1010010 |
| 33 |
100001 |
83 |
1010011 |
| 34 |
100010 |
84 |
1010100 |
| 35 |
100011 |
85 |
1010101 |
| 36 |
100100 |
86 |
1010110 |
| 37 |
100101 |
87 |
1010111 |
| 38 |
100110 |
88 |
1011000 |
| 39 |
100111 |
89 |
1011001 |
| 40 |
101000 |
90 |
1011010 |
| 41 |
101001 |
91 |
1011011 |
| 42 |
101010 |
92 |
1011100 |
| 43 |
101011 |
93 |
1011101 |
| 44 |
101100 |
94 |
1011110 |
| 45 |
101101 |
95 |
1011111 |
| 46 |
101110 |
96 |
1100000 |
| 47 |
101111 |
97 |
1100001 |
| 48 |
110000 |
98 |
1100010 |
| 49 |
110001 |
99 |
1100011 |
| 50 |
110010 |
100 |
1100100 |
10 進法の仕組み(2 進法も考え方は同じ)
1024 の場合
1024 の計算方法
| 1000 |
× |
1 |
= |
1000 |
全部を足して 1000 + 0 + 20 + 4 = 1024 となる |
| 100 |
x |
0 |
= |
0 |
| 10 |
x |
2 |
= |
20 |
| 1 |
x |
4 |
= |
4 |
2 進法の仕組み
1011 の計算方法(10 進法へ変換)
| 8 |
× |
1 |
= |
8 |
全部を足して 8 + 0 + 2 + 1 = 11 となる |
| 4 |
x |
0 |
= |
0 |
| 2 |
x |
1 |
= |
2 |
| 1 |
x |
1 |
= |
1 |
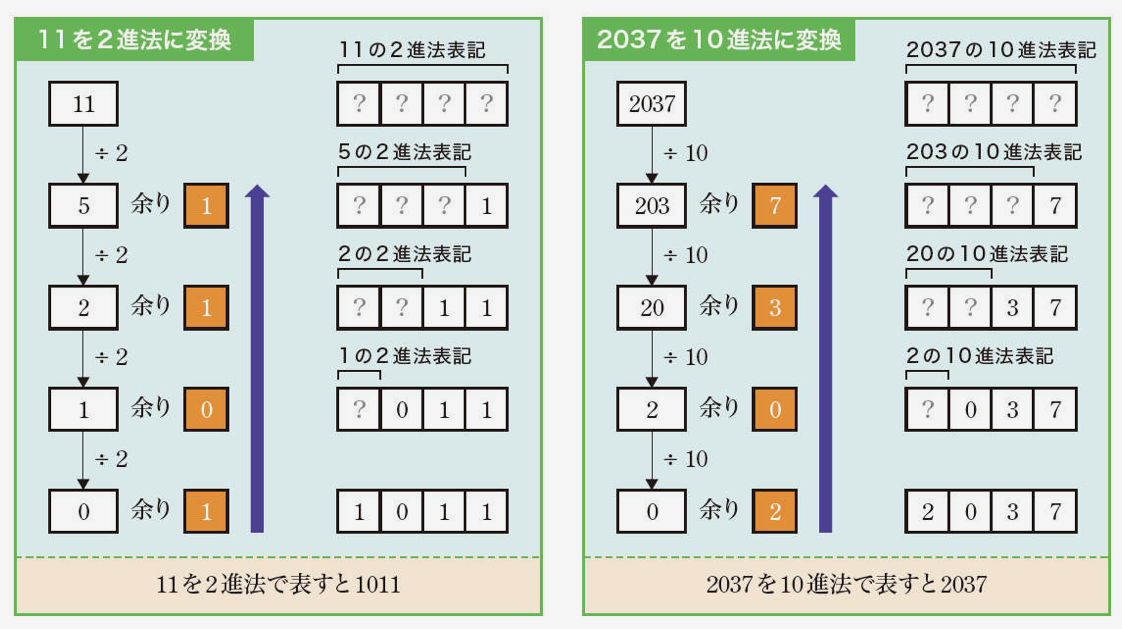
10進法から2進法 / 10進法から10進法
数が 0 になるまで 2 で割った余りを書いていき、それを下から読むことで 10 進法を 2 進法に変換することができます。
10進法を2進法に変換するプログラム (c++)
binary.cpp
#include <iostream>
#include <string>
using namespace std;
int N;
string Answer = "";
int main() {
cin >> N;
while (N >= 1) {
// N % 2 は N を 2 で割った余り (例:N=13 の場合 1)
// N / 2 は N を 2 で割った値の整数部分 (例:N=13 の場合 6)
if (N % 2 == 0) Answer = "0" + Answer;
if (N % 2 == 1) Answer = "1" + Answer;
N = N / 2;
}
cout << Answer << endl; //出力
return 0;
}
コンパイル、実行
# コンパイル、実行
g++ -o binary binary.cpp && ./binary
# 標準入力で 4 を入力する
4
# 標準出力で 100 が出力される
100


